Échange de clés Diffie-Hellman

HISTOIRE ET USAGE

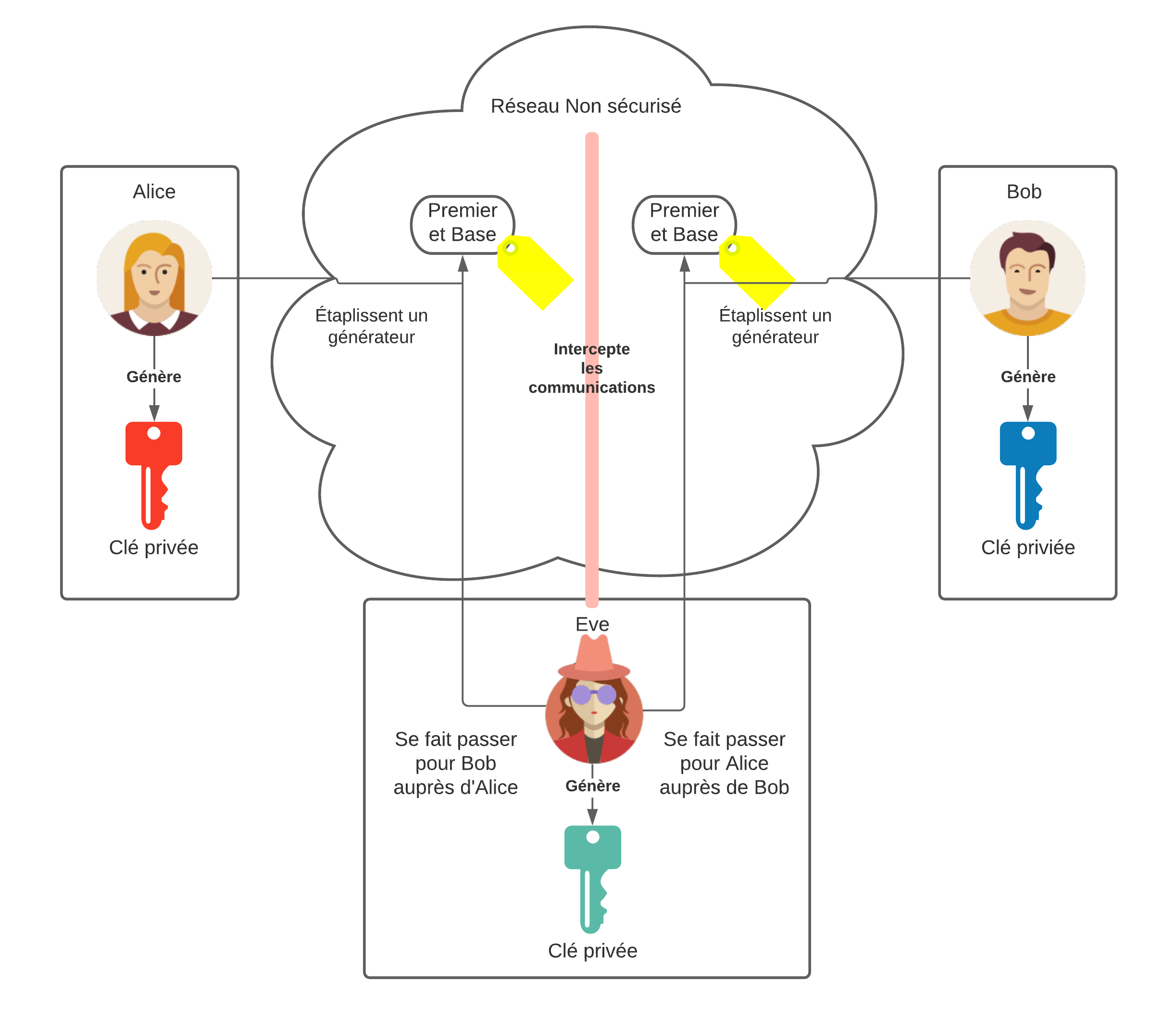
L'échange de clé Diffie-Hellman est une des premières méthodes d'échange sécurisé de clés cryptographiques impliquant la présence d'une clé publique et d'une clé privée. Ce protocole a été publié en 1976 par Whitfield Diffie et Martin Hellman, en s'inspirant des travaux de Ralph Merkle, l'un des inventeurs de la cryptographie par clé publique. En effet, Diffie-Hellman se base sur le puzzle de Merkle, qui se trouve être un jeu où un expéditeur envoie un certain nombre d'énigmes cryptographique à un receveur, qui devra effectuer des calculs pour récupérer un identifiant et une clé de session. Dans ce jeu, le receveur va choisir au hasard une des énigmes qui lui a été envoyé, la résoudre, puis renvoyer l'identifiant à l'expéditeur dans le but de lui notifier de la résolution de l'énigme choisie. L'expediteur recevant cet identifiant sait donc quelle clé de session sera utilisée pour communiquer avec le destinataire. L'intérêt d'un tel mécanisme est qu'un attaquant écoutant les échanges entre les 2 personnes, va peut-être intercepter l'identifiant, mais devra résoudre les énigmes pour récupérer la bonne clé de session, ce qui est beaucoup plus difficile que la résolution d'une seule énigme par le receveur.

Les inventeurs de la méthode Diffie-Hellman

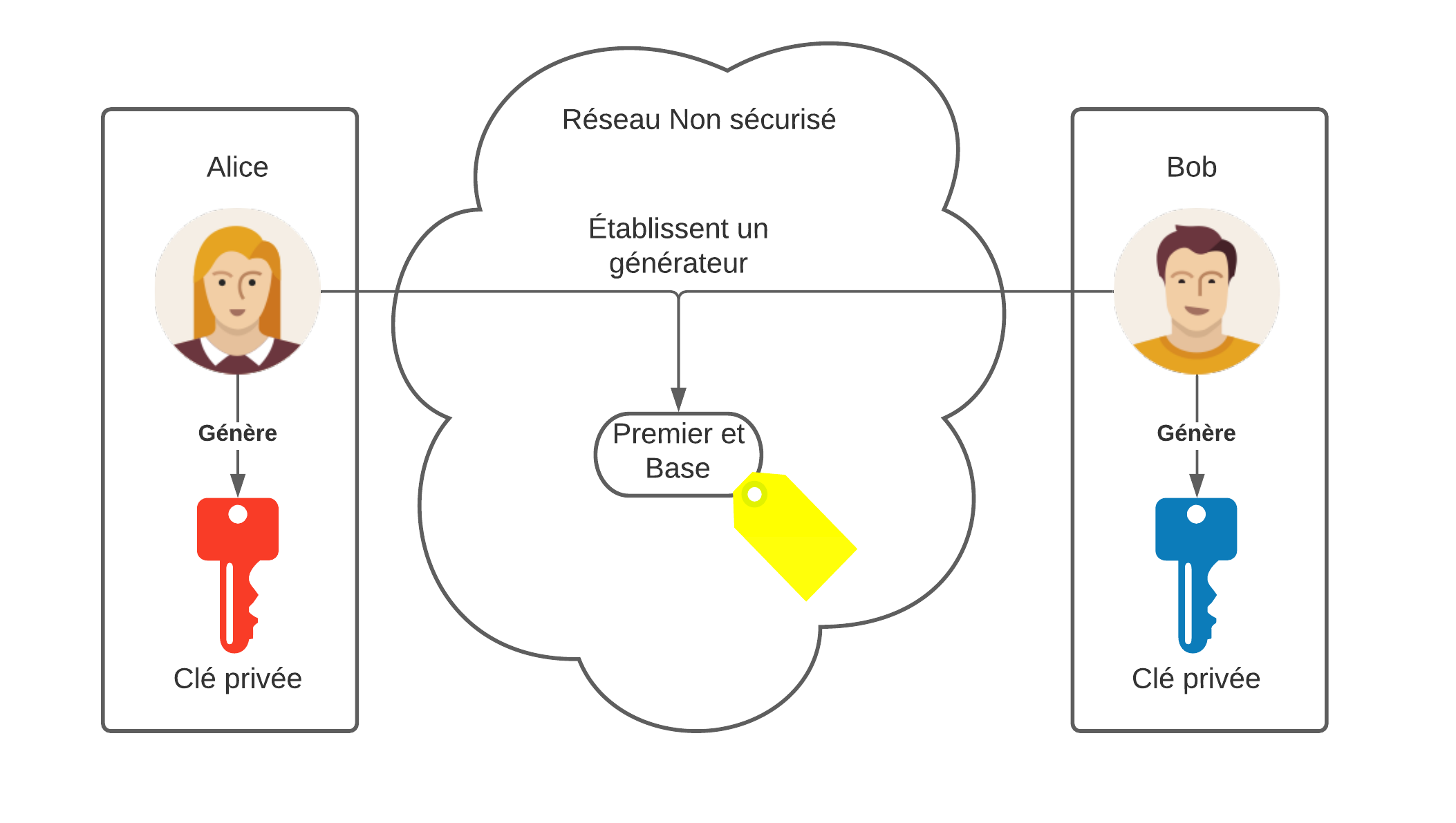
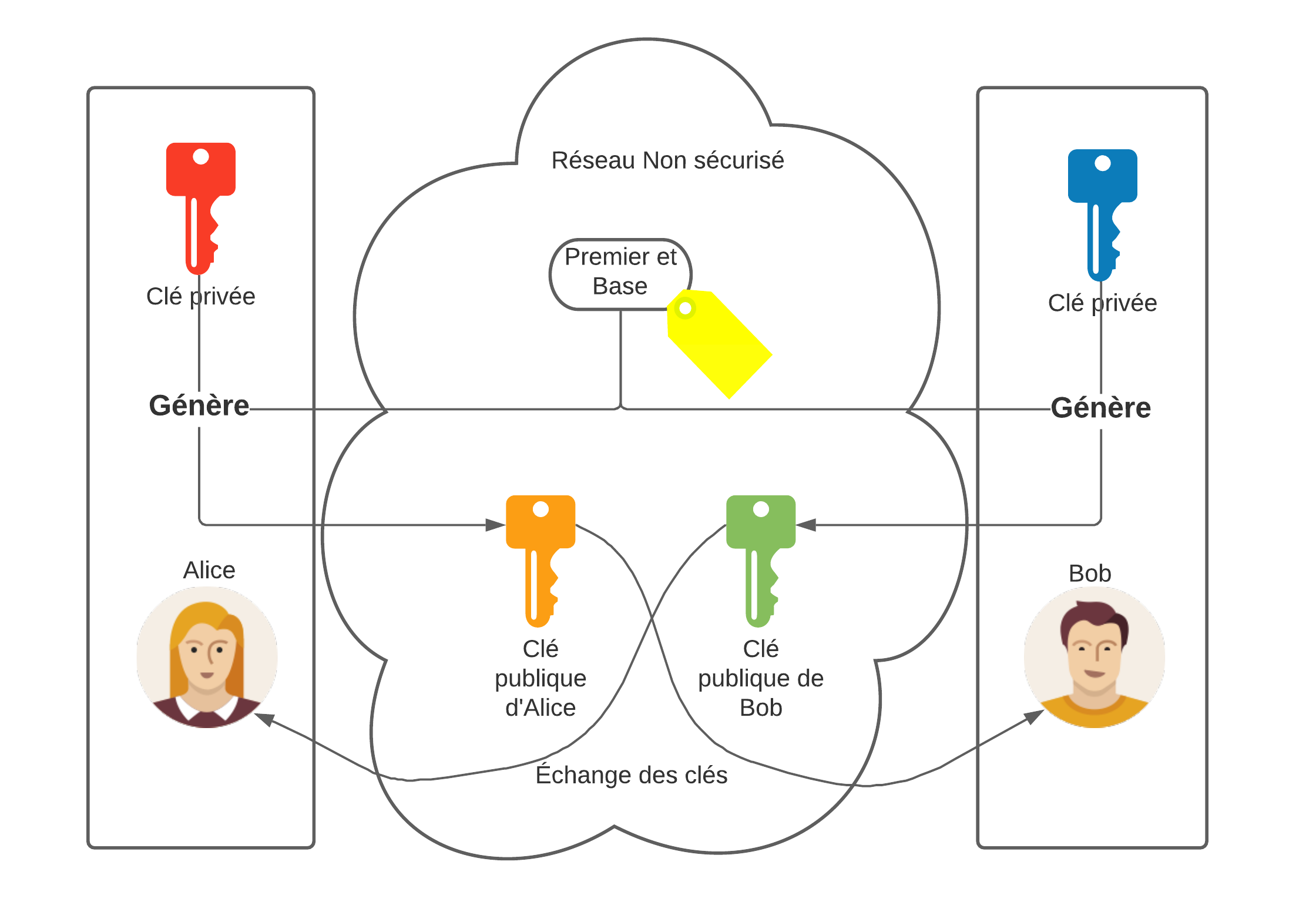
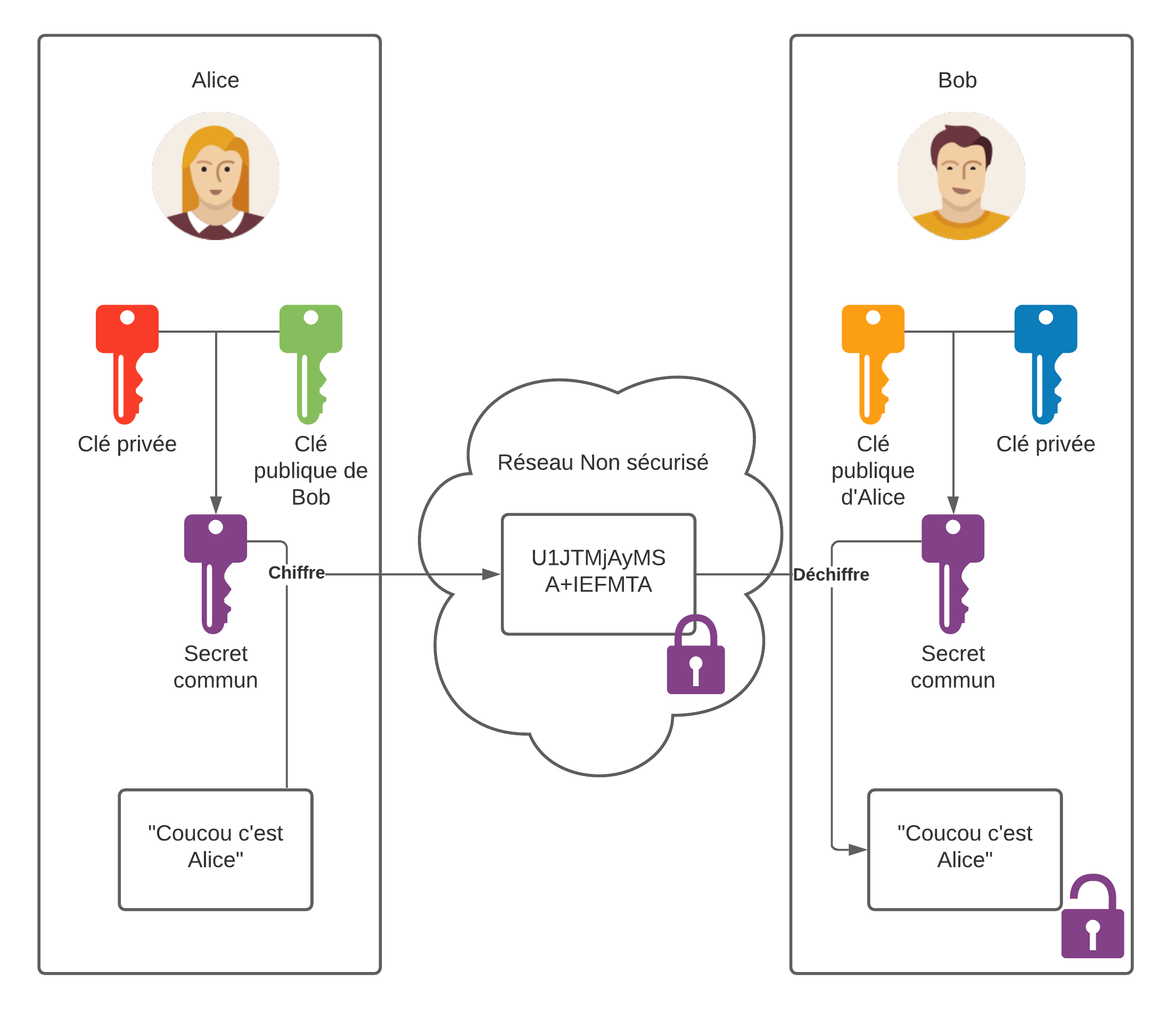
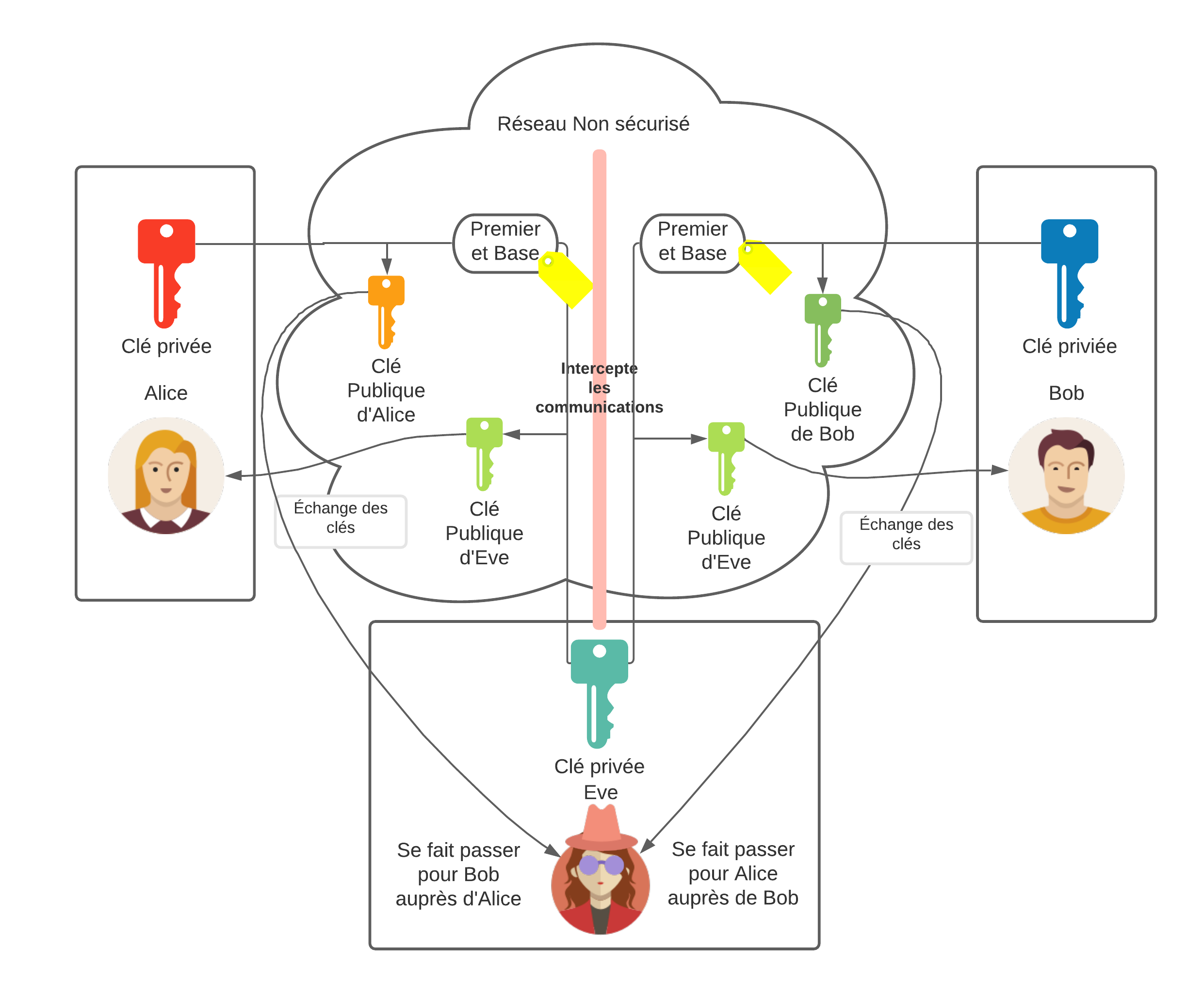
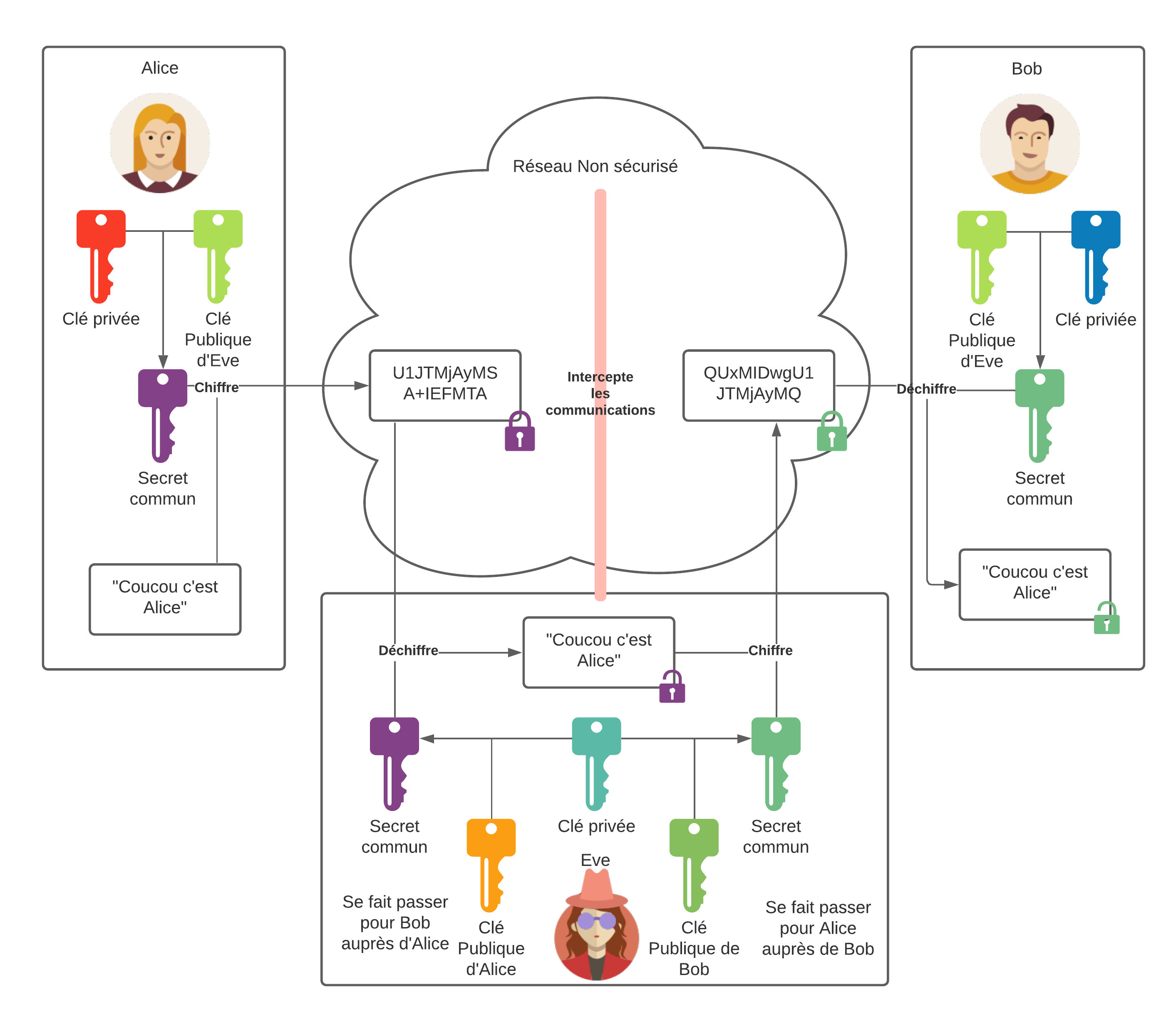
Diffie et Hellman ont complexifiés ce mécanisme de sécurité pour le rendre plus robuste et donc de pouvoir transmettre un secret dans un canal non-sécurisé. Effectivement, ce secret partagé combiné avec la clé privé de chacun des 2 parties, donnera la clé symmétrique utilisé pour la communication chiffrée.

Aujourd'hui, nous utilisons Diffie-Hellman au quotidien, puisque ce protocole peut être utilisé pour transmettre des clés de manière sécurisé pour d'autres protocoles, tels que TLS, IPSec ou encore SSH. Étant donné que l'algorithme tend à créer une clé symmétrique, l'échange de clé Diffie-Hellman peut donc assurer le transfert de clés pour les algorithmes symétriques (algorithmes très utilisés pour transférer des données plus rapidement que les algorithmes asymétriques) et s'associer à d'autres protocoles pour fournir ce service de transfert sécurisé de clés. Cependant, Diffie-Hellman n'assure pas l'authentification des 2 parties lors de l'échange, il peut en conséquence, être appelé avec une méthode d'authentification (signature électronique par exemple).

Base Mathématiques

Première implémentation

Soit $p$ un nombre premier.
On se place dans le groupe multiplicatif ($\mathbf{Z}/p\mathbf{Z}$, $*$) d'ordre $p$.
Soit $g$ $\lt$ $p$.

Dans le protocole d'échange de clé de Diffie-Hellman, $p$ et $g$ sont connus de tous.
Le secret partagé que les parties cherchent à obtenir sera secret avec $1$ $\lt$ secret $\lt$ $p$ $-$ $1$.

Exemple protocole

Prenons le cas simple où deux personnes $A$ et $B$ souhaitent obtenir un secret partagé.

Soient $a$ la clé privée de $A$ et $b$ la clé privée de $B$.

Les clés privées de chacun sont définies aléatoirement. Les clés privées ne doivent être connues que de leur détenteur.

L'obtention de clé publique à partir de la clé privée se fait comme suit :
Soient $K_A$ la clé publique de $A$ et $K_B$ la clé publique de $B$.

On a : $K_A$ = $g^a$ $[ p ]$
$K_B$ = $g^b$ $[ p ]$

Soient :

p = 541
g = 10

a = 5
b = 7

Calcul des clés publiques :
$K_A$ :

K_A = g^a % p
print("K_A = ", K_A)

K_A =  15

$K_B$ :

K_B = g^b % p
print("K_B = ", K_B)

K_B =  13

On pose secret $= K_B^a$ $ [ p ]$ = $K_A^b$ $[ p ]$

Le secret est le même pour $A$ et pour $B$, même si le calcul pour l'obtenir n'est pas le même. C'est pour cela que l'on parle de secret partagé.

Vérification:
$K^a_B$ $[ p ] =$ $(g^b$ $[ p ] )^a$ $[ p ] =$ $g^{ba}$ $ [ p ] =$ $g^{ab}$ $[ p ] =$ $(g^a$ $[ p ] )^b$ $[ p ] =$ $K^b_A$ $[ p ]$

Pour calculer le secret, $A$ et $B$ vont échanger leur clé publique.

Calcul du secret :

secret_A = K_B^a % p
secret_B = K_A^b % p

if (secret_A == secret_B ):
    print("Diffie Hellman ça marche !! secret : ", secret_A)
else :
    print ("Diffie Hellman c'est nul :O")

Diffie Hellman ça marche !! secret :  8

Le calcul $g^{ba}$ $ [ p ] =$ $g^{ab}$ $[ p ]$ est extrêmement long à calculer si les chiffres sont assez grands. La fiabilité de l'échange de clé Diffie-Hellman repose sur le fait qu'il est impossible de trouver $b$ si on possède $g$, $p$ et $K_B$ ($= g^b$ $[ p ]$ ) avec les moyens actuels.
Ce problème est appelé le problème du logarithme discret.

A plusieurs

Plusieurs personnes peuvent souhaiter partager un secret. Cela est aussi possible avec Diffie-Hellman.
Soient N personnes souhaitant partager un secret de clé privée $a$, $b$, $c$, ... Il y a donc N clés privées.
$g$ et $p$ sont connus de tous.

Etape 1 à N-1 : chacun des participants sauf vous mettent le secret temporaire à la puissance de leur clé privée. Ici, une fuite du secret en construction n'a aucune incidence. En effet, même en possession de $g^{abc}$ et de $g^{bcd}$, il est impossible de déduire $g^{abcd}$.
Etape N : Elaboration du secret : vous ajoutez à l'équation votre clé secrète.

Il y a donc N étape pour établir le secret. Etant confidentiel, il ne peut être partagé et doit donc être recalculé pour chacun des participants. L'associativité permet d'obtenir le même secret : on a bien $g^{(ab)c}$ $=$ $g^{a(bc)}$. On note de plus que la multiplication est ici commutative.
Il faut donc N étapes $*$ N personnes pour que tout le monde obtienne le secret dans le pire des cas.

Pour diminuer le nombre d'étapes, il est possible de dupliquer les clés intermédiaires.

Exemple :

c = 11
K_C = g^c % p
print("K_C = ", K_C)

pre_secret_A = K_B^c % p #Etape 1 : clé publique de B, Etape 2 : clé privée de C
pre_secret_B = K_C^a % p #Etape 1 : clé publique de C, Etape 2 : clé privée de A
pre_secret_C = K_A^b % p #Etape 1 : clé publique de A, Etape 2 : clé privée de B

secret_A = pre_secret_A^a % p #Etape 3 : exposant de A
secret_B = pre_secret_B^b % p #Etape 3 : exposant de B
secret_C = pre_secret_C^c % p #Etape 3 : exposant de C

if (secret_A == secret_B and secret_B == secret_C ):
    print("Diffie Hellman ça marche !! secret : ", secret_A)
else :
    print ("Diffie Hellman c'est nul :O")

K_C =  1
Diffie Hellman ça marche !! secret :  3

Autres espaces

La première démonstration de l'échange de clé Diffie-Hellman se faisait effectivement dans $\mathbf{Z}/p\mathbf{Z}$ où $p$ est premier. Cependant, le même principe est applicable dans un groupe cyclique fini quelconque ou même sur une courbe elliptique.
Il faut donc se placer dans un groupe fini et savoir le définir pour pouvoir ensuite calculer clé privée et secret.

Limitation crypto

Les difficultés de l'échange de clé de Diffie-Hellman sont les mêmes que pour toute la crypto.
Dans le cas d'un groupe $\mathbf{Z}/p\mathbf{Z}$ où $p$ est premier, la première difficulté réside dans le fait de trouver un nombre premier (assez grand).
Il est ensuite question de génération d'aléa pour les clés privées des parties.

Fonctions utilisées après

def chiffrement (secret, base, premier):
    return (base ** secret) % premier

def calcul_secret_partagé (secret_partagé, secret_privé, nombre_premier_partagé):
    return (secret_partagé ** secret_privé) % nombre_premier_partagé

Example d'implémentation

Cas classique

Dans cette example Alice et Bob s'envoient des messages secret sur un réseau non sécurisé en utilisant Diffie-Hellman.

Eve fait une attaque Man in the Middle.

Ce processus ce fait en trois étapes :

1) Initialisation

Alice et Bob prépare chacun une clé privée :

clé_privée_d_Alice = 100
clé_privée_de_Bob = 200

Ensuite ils se mettent d'accord sur deux valeurs :

base_partagé = 1000
premier_partagé = 42863

2) Calcul et Échange des clés publiques

Alice calcul et envoye sa clé publique:

clé_publique_d_Alice = chiffrement (clé_privée_d_Alice, base_partagé, premier_partagé) 
print("Clé publique d'Alice : ", clé_publique_d_Alice)

Clé publique d'Alice :  8425

Bob calcul et envoie sa clé publique à Alice:

clé_publique_de_bob = chiffrement (clé_privée_de_Bob, base_partagé, premier_partagé) 
print("Clé publique de Bob : ", clé_publique_de_bob)

Clé publique de Bob :  42360

3) Chacun calcul son secret commun

Alice calcul le secret partagé

résultat_d_Alice = calcul_secret_partagé(clé_publique_de_bob, clé_privée_d_Alice, premier_partagé)
résultat_d_Alice

4195

Bob calcul le secret partagé

résultat_de_Bob = calcul_secret_partagé(clé_publique_d_Alice, clé_privée_de_Bob, premier_partagé)
résultat_de_Bob

4195

Ils ont bien le même secret partagé, sans l'avoir envoyé sur le réseau

print (résultat_d_Alice," == ", résultat_de_Bob)

4195  ==  4195

Alice et Bob peuvent donc s'envoyer des messages en utilisant le secret commun.

Exemple d'implémentation d'attaque

1) Initialisation

Alice et Bob prépare chacun une clé privée :

clé_privée_d_Alice = 100
clé_privée_de_Bob = 200

Eve prépare aussi une clé privée

clé_privée_d_Eve = 300

Pendant ce temps Eve intercepte la communication entre Bob et Alice.

Elle se fait passer pour Bob auprès d'Alice et inverssement.

Eve établie un nombre premier et une base partagé avec Alice et Bob. (Dans cet exemple on garde les mêmes pour Alice et Bob)

base_partagé = 1000
premier_partagé = 42863

2) Caclcul et Échange des clés publiques

Alice calcule et envoie sa clé publique à Bob (Mais l'envoie en fait à Eve):

clé_publique_d_Alice = chiffrement (clé_privée_d_Alice, base_partagé, premier_partagé) 
print("Clé publique d'Alice : ", clé_publique_d_Alice)

Clé publique d'Alice :  8425

Bob calcul et envoie sa clé publique à Alice (Mais l'envoie en fait à Eve):

clé_publique_de_Bob = chiffrement (clé_privée_de_Bob, base_partagé, premier_partagé) 
print("Clé publique de Bob : ", clé_publique_de_bob)

Clé publique de Bob :  42360

Eve a donc reçue la clé publique d'Alice et de Bob.

Elle calcule sa clé publique pour Alice et pour Bob et leur envoie.

clé_publique_d_Eve = chiffrement (clé_privée_d_Eve, base_partagé, premier_partagé) 
print("Clé publique d'Eve pour Alice et Bob : ", clé_publique_d_Eve)

Clé publique d'Eve pour Alice et Bob :  5662

3) Chacun calcul son secret commun

Alice calcul le secret commun avec Bob (Mais en fait c'est avec Eve):

résultat_d_Alice = calcul_secret_partagé(clé_publique_d_Eve, clé_privée_d_Alice, premier_partagé)
résultat_d_Alice

5450

Eve calcul le secret commun pour sa communication avec Alice :

résultat_d_Eve_avec_Alice = calcul_secret_partagé(clé_publique_d_Alice, clé_privée_d_Eve, premier_partagé)
résultat_d_Eve_avec_Alice

5450

Bob calcul le secret commun avec Alice (Mais en fait c'est avec Eve):

résultat_de_Bob = calcul_secret_partagé(clé_publique_d_Eve, clé_privée_de_Bob, premier_partagé)
résultat_de_Bob

41304

Eve calcul le secret commun pour sa communication avec Bob :

résultat_d_Eve_avec_Bob = calcul_secret_partagé(clé_publique_de_Bob, clé_privée_d_Eve, premier_partagé)
résultat_d_Eve_avec_Bob

41304

Eve peut maintenant déchiffré la communication entre Alice et Bob

Conclusion

L'Échange de clé avec Diffie-Hellman est un protocol assez sécurisé.

En générale la base utilisée est un très grand nombres qui permet d'éviter les attaques par force brute. Aujourd'hui, on estime que codé la base sur 512 bits ou 718 bits donne un protocol trop faible, 1024 bits n'est pas suffissant n'ont plus face à des organisations étatiques. À partir de 2048 on estime que le protocole est sûre. Néanmoins il faut faire attention aux nouvelles technologies comme les ordinateurs quantitques qui pourraient mettre à mal Diffie-Hellman.

L'attaque "man in the midle" que nous montrons met en perspective la place des outils cryptographiques dans la sécurité informatique. Dans notre example le principe mathématique n'a pas été cassé mais contourné. La force cryptographique d'une solution est tout aussi importante que son implémentation dans les réseaux.